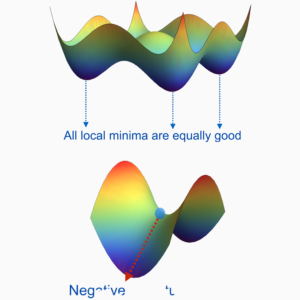
Prototypical 21st-century data science problems are endowed with the following characteristics: (1) large-scale, (2) high-dimensional, and (3) nonconvex. For instance, the efficient training of realistic neural networks amounts to solving a massive-scale and nonconvex optimization problem with millions of unknown variables. With the ever-increasing dimension, volume, and complexity of the data collected and assimilated, the performance of modern machine learning methods crucially relies on the particular choice of data representation. Over the past few decades, we have witnessed the revolution of (deep) representation learning, mainly driven by data and computation. However, the underlying principles behind its empirical success largely remain a mystery. One of the major challenges pertains to the nonlinearity of the models, which results in highly nonconvex optimization problems which can be NP-hard in the worst case. Nonetheless, empirical evidence suggests that often the symmetric properties of the problems and intrinsic low-dimensional structures of the data often alleviate the hardness of these problems, so simple heuristic and local nonconvex optimization methods often work surprisingly well for learning succinct and even deep hierarchical representations. In this proposal, we aim to bridge the gap between practice and theory of modern representation learning methods, by studying the geometric properties of optimization landscapes and exploiting the low-dimensional structures of the data. The new geometric insights and data structure will not only explain what kind of representations can be learned through optimization, but also shed light on the principled design of better learning models and the development of efficient, globally convergent algorithms. Leveraging this framework, we will study a wide spectrum of representation learning problems ranging from supervised to unsupervised learning, and we will study the robustness and transferability of these learning procedures through an understanding of the learned representations.
People

Funding: $75K (2022)
Goal: The proposed work will contribute to the development of the foundations of machine learning and efficient computational methods with rigorous guarantees, which well aligns with the Methodological Foundation pillar.
Token Investors: Quing Qu, Laura Balzano, Albert Berahas, Eunshin Byon, Salar Fattahi
Project ID: 1012





